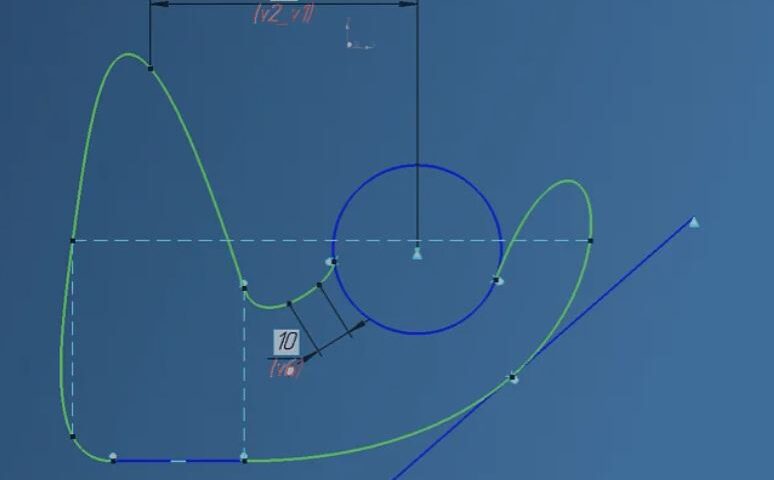
В основе параметрического моделирования лежит идея управления формой объекта не напрямую через координаты, а через систему геометрических и численных ограничений. Такие ограничения определяют, какие элементы модели должны быть зафиксированы, какими отношениями они связаны и как они могут изменяться при редактировании.
Поддержка геометрических ограничений внутри ядра позволяет интерпретировать модель не как набор разрозненных примитивов, а как логически связанный объект, поведение которого предсказуемо и управляемо. Это критично в инженерных системах, где даже небольшое отклонение от проектных условий может повлиять на работоспособность изделия.
Классификация геометрических ограничений
Геометрические ограничения представляют собой правила, которым должна соответствовать геометрия модели. Они могут быть условно разделены на следующие группы:
– Позиционные: совпадение, фиксация точки, принадлежность прямой или поверхности.
– Ориентационные: параллельность, перпендикулярность, тангенциальность.
– Размерные: расстояние между точками, длина отрезка, радиус дуги, угол между элементами.
– Симметричные: симметрия относительно оси или точки.
– Зависимости: равенство размеров, пропорциональные связи, формулы.
Каждое ограничение задаёт часть поведения модели и исключает нежелательные степени свободы. Например, если задать отрезку горизонтальность, его нельзя будет повернуть произвольно, а при изменении длины он останется параллелен оси X.
Представление ограничений внутри ядра
Внутри геометрического ядра ограничения хранятся в виде системы алгебраических и геометрических уравнений.
Каждое ограничение формализуется как математическая функция, аргументами которой являются параметры геометрических объектов: координаты точек, параметры кривых, радиусы, углы и т.д. Например:
- Ограничение параллельности: разность направляющих векторов двух отрезков должна быть нулевой.
- Ограничение касания: расстояние между точкой на одной кривой и касательной к другой кривой должно быть минимальным и равно нулю.
В совокупности ограничения образуют систему уравнений, которую решает специализированный решатель параметрических задач.
Как ядро определяет, что можно двигать
При редактировании модели (например, перемещении точки, изменении размера) ядро должно интерпретировать действия пользователя в контексте всех заданных ограничений.
Сначала анализируется граф зависимостей между объектами. Определяются:
– какие элементы зафиксированы,
– какие параметры являются свободными,
– какие параметры выражены через другие.
Решатель вычисляет допустимое изменение, которое сохраняет корректность модели. Если пользователь пытается изменить элемент, связанный ограничением, система либо блокирует изменение, либо перестраивает остальные элементы, чтобы удовлетворить всем условиям.
Пример: если две окружности должны касаться, перемещение одной из них вызывает перестроение второй — чтобы касание сохранялось.
Алгоритм работы решателя
Решатель ограничений реализует следующие этапы:
- Сбор системы уравнений: для всех ограничений формируются выражения.
- Анализ зависимостей: определяются переменные, подлежащие вычислению, и фиксированные параметры.
- Определение степени свободы: решатель проверяет, не переопределена или не недоопределена система.
- Численное решение: с помощью итерационных или прямых методов находится значение параметров, удовлетворяющее всем условиям.
- Контроль точности: проверяется допустимость вычисленных значений в рамках допусков.
- Обновление модели: пересчитываются координаты и форма геометрии.
Такая схема позволяет гибко управлять моделью, минимизируя ошибки и обеспечивая устойчивое поведение при редактировании.
Конфликты и недоопределённость
Система ограничений может быть:
– полностью определённой — единственное корректное решение;
– недоопределённой — несколько решений, необходимо зафиксировать дополнительные параметры;
– переопределённой — противоречивые ограничения, система несовместна.
Решатель должен диагностировать эти состояния и сообщать пользователю о необходимости корректировки модели: например, отключить одно из конфликтующих ограничений или добавить недостающие связи.
В случае недоопределённости поведение модели может быть неоднозначным — при редактировании она может перестроиться не так, как ожидается. Поэтому ядро может применять эвристики для выбора наиболее “естественного” решения.
Поддержка ассоциативности и истории построения
Геометрические ограничения часто задаются не на финальные элементы, а на стадии построения — в эскизе или дереве операций.
Ядро должно обеспечивать:
– согласованность ограничений при добавлении и удалении операций;
– возможность отката к исходной геометрии;
– ассоциативность между параметрами и результатом.
Это позволяет строить управляемые модели, в которых изменение базовых параметров автоматически обновляет все зависимые элементы.
Пример: изменение ширины в эскизе приводит к перестроению трёхмерного выдавливания, в котором эта ширина участвует как параметр.
Работа с несколькими системами координат
В сборках или при моделировании в разных плоскостях элементы могут располагаться в различных системах координат.
Ядро должно корректно интерпретировать ограничения между объектами, находящимися в разных координатных пространствах:
– трансформировать координаты;
– проецировать ограничения на общую плоскость;
– учитывать зависимости между осями и плоскостями.
Это особенно актуально при работе с подмоделями, компонентами сборок, симметричными и зеркальными элементами.
Интерактивность и производительность
Для поддержки интерактивной работы решатель должен выполнять пересчёт ограничений в режиме реального времени.
Это требует:
– минимизации количества пересчитываемых уравнений;
– хранения кэшированных решений;
– использования адаптивных итерационных алгоритмов.
Решатель также должен предсказывать возможные конфликты заранее — например, при перетаскивании объекта, ещё до завершения действия пользователя. Это достигается за счёт предварительного анализа степени свободы и зависимости элементов.
Поддержка пользовательских ограничений
Некоторые системы позволяют создавать пользовательские ограничения, выражаемые через формулы, логические выражения, условия.
Пример: «расстояние от точки A до линии B не должно превышать заданный параметр».
Гибкая архитектура решателя должна поддерживать расширение набора ограничений, в том числе:
– ввод через скрипты или выражения;
– добавление новых типов геометрии;
– настройку допусков и условий.
Это делает систему открытой и адаптируемой под задачи конкретного проектирования или отраслевого применения.
Связь с другими подсистемами
Геометрические ограничения — основа для:
– параметризации модели;
– конфигурирования изделий;
– генерации спецификаций;
– адаптивных шаблонов.
Они также используются при синхронизации модели с расчетными и производственными модулями: ограничения могут быть интерпретированы как граничные условия или допуски.
Таким образом, полноценная поддержка ограничений внутри ядра — не просто удобство, а архитектурное условие для построения управляемых, воспроизводимых и инженерно значимых моделей.